En este post hablaré sobre fractales, y más específicamente del triángulo de Sierpinski.
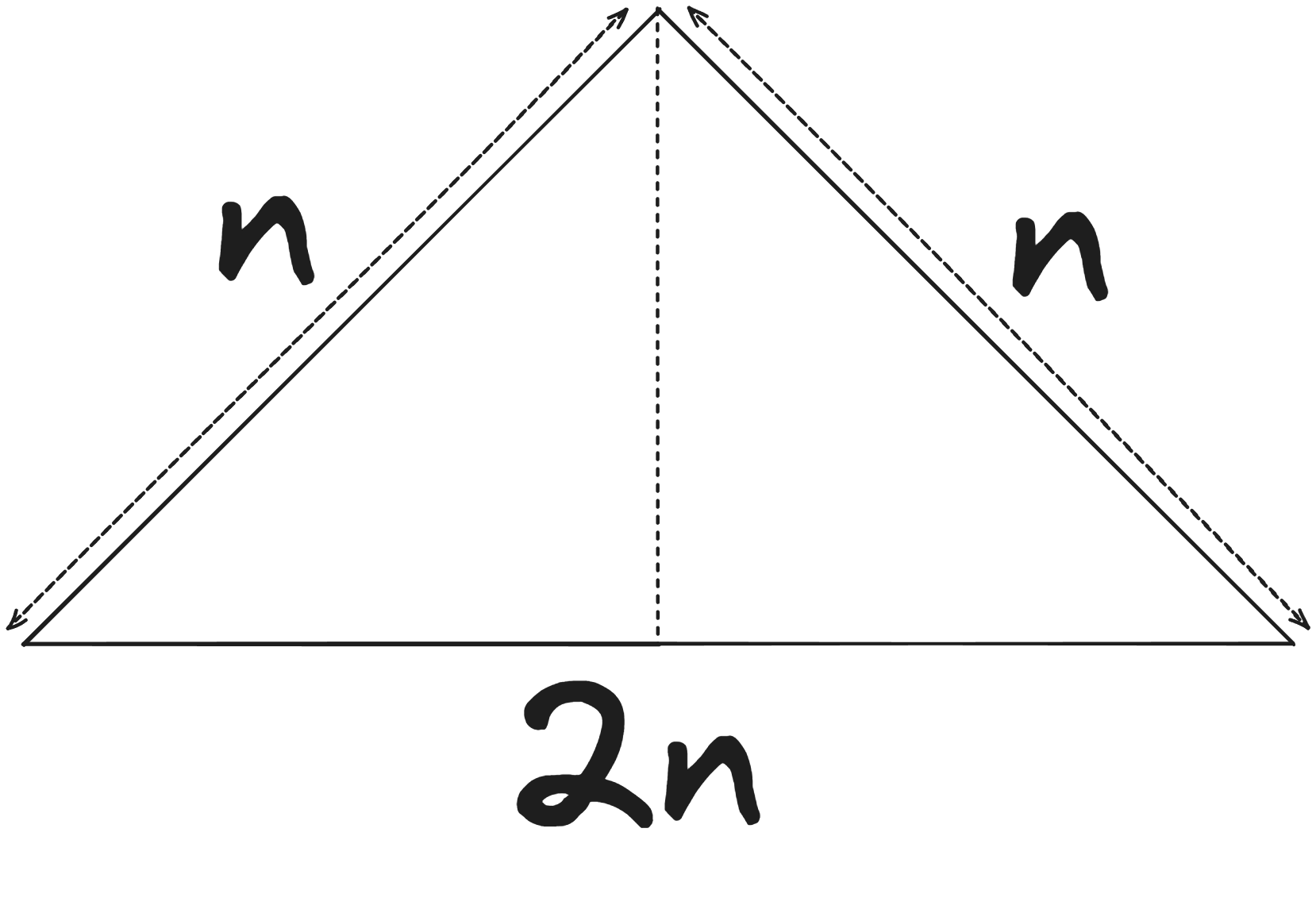
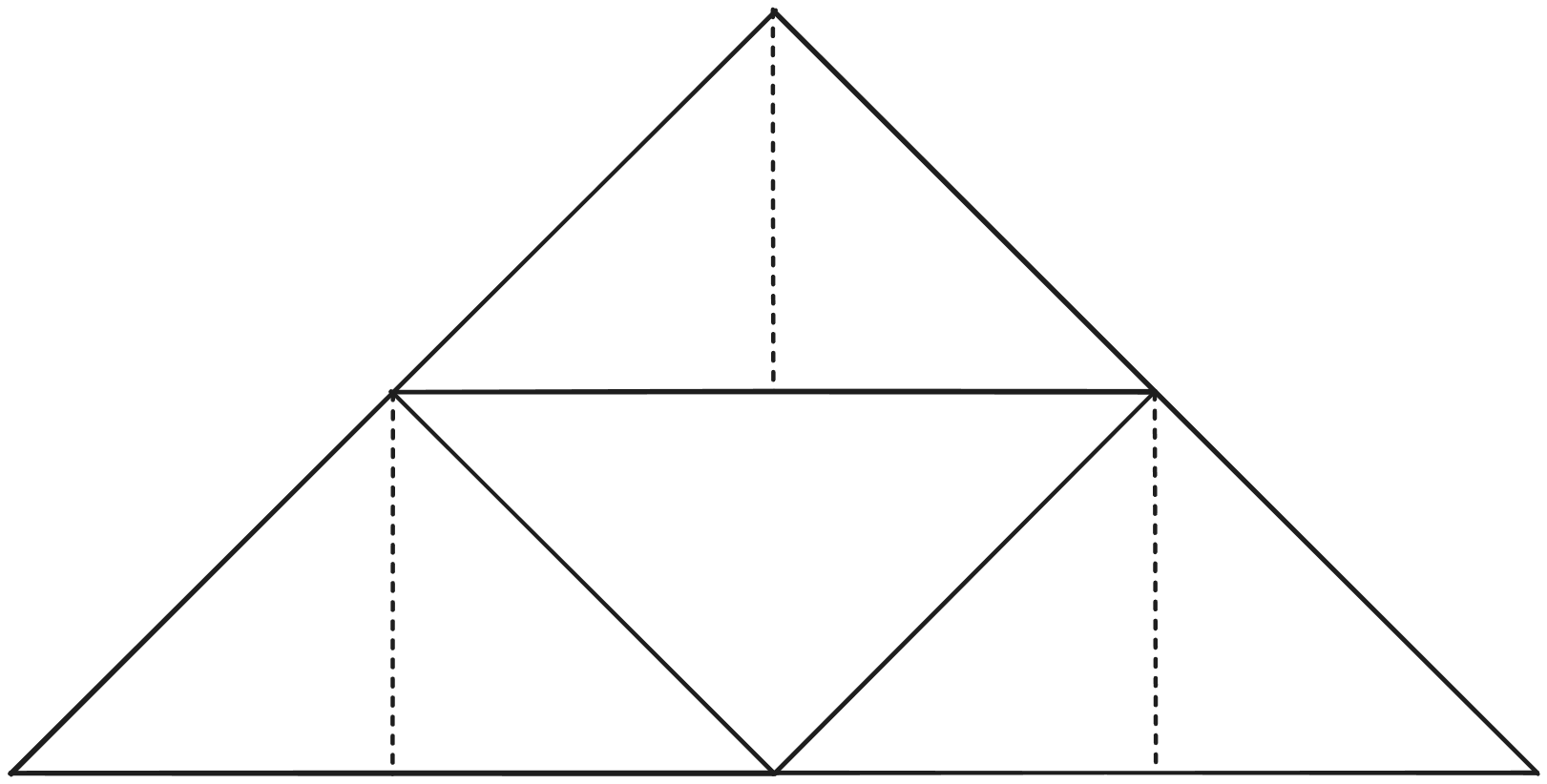
Hoy, vengo a mostrarles como construir triángulos de Sierpinski proyectando líneas, todo suponiendo un triángulo equilátero. Dividido en dos, tendremos dos triángulos rectángulos que serán congruentes, solo están invertidos. Algo así:
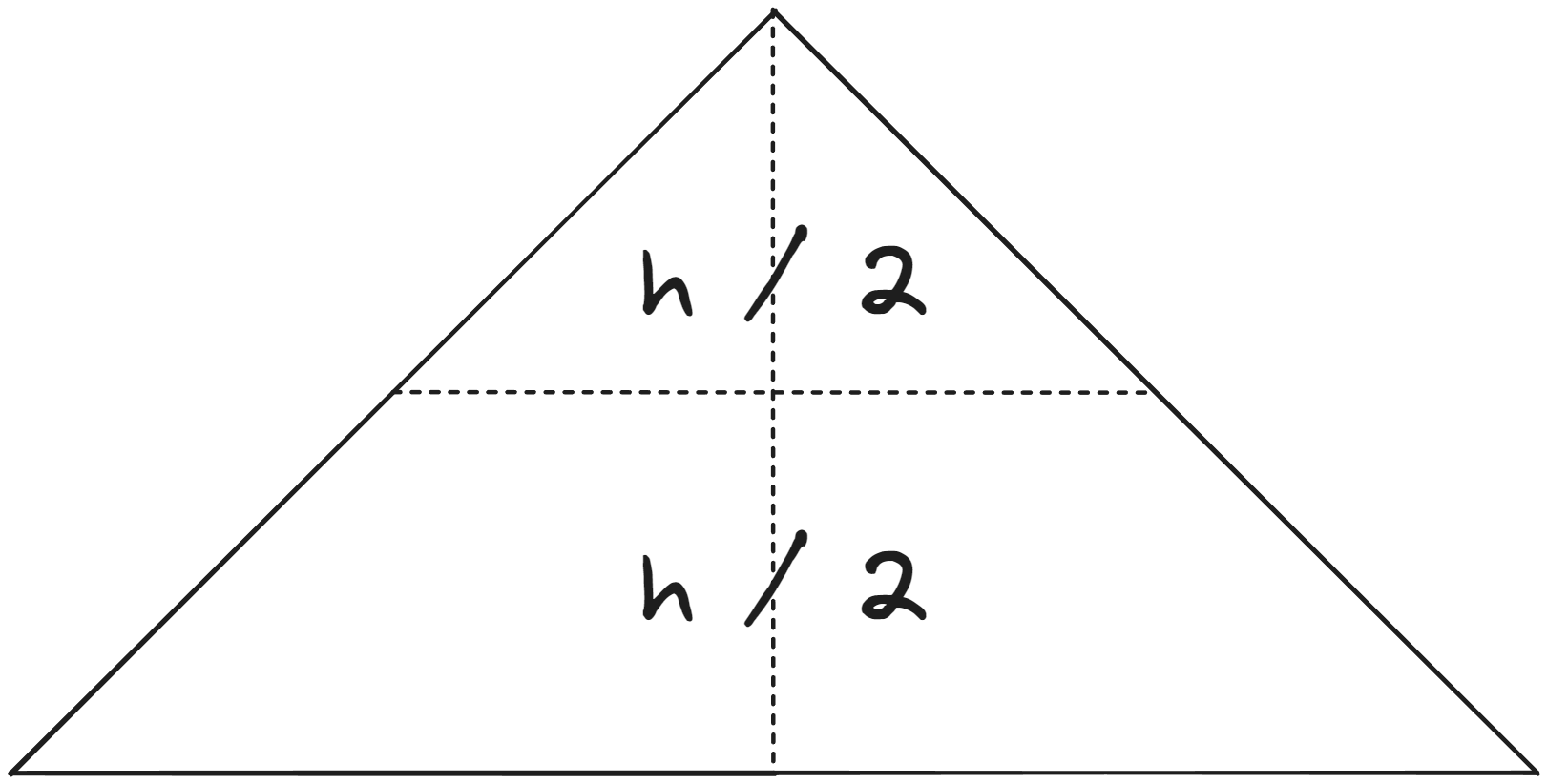
Ahora, para poder completar la primera iteración, dividimos la proyección vertical al centro de la base horizontalmente en dos. La gracia de hacer esto es que ahora tenemos dos proyecciones que nos dicen perfectamente en donde poner nuestras líneas rectas.
Al marcar las líneas resultantes queda lo siguiente, y podemos seguir proyectando desde el punto más alto de cada triángulo nuevo. Lo bonito es que estos cuatro triángulos interiores son escalables por cierto factor y podemos obtener el original (hay cuatro triángulos, cada uno es 1/4 del original), o sea, son semejantes.
La siguiente iteración se ve algo así:
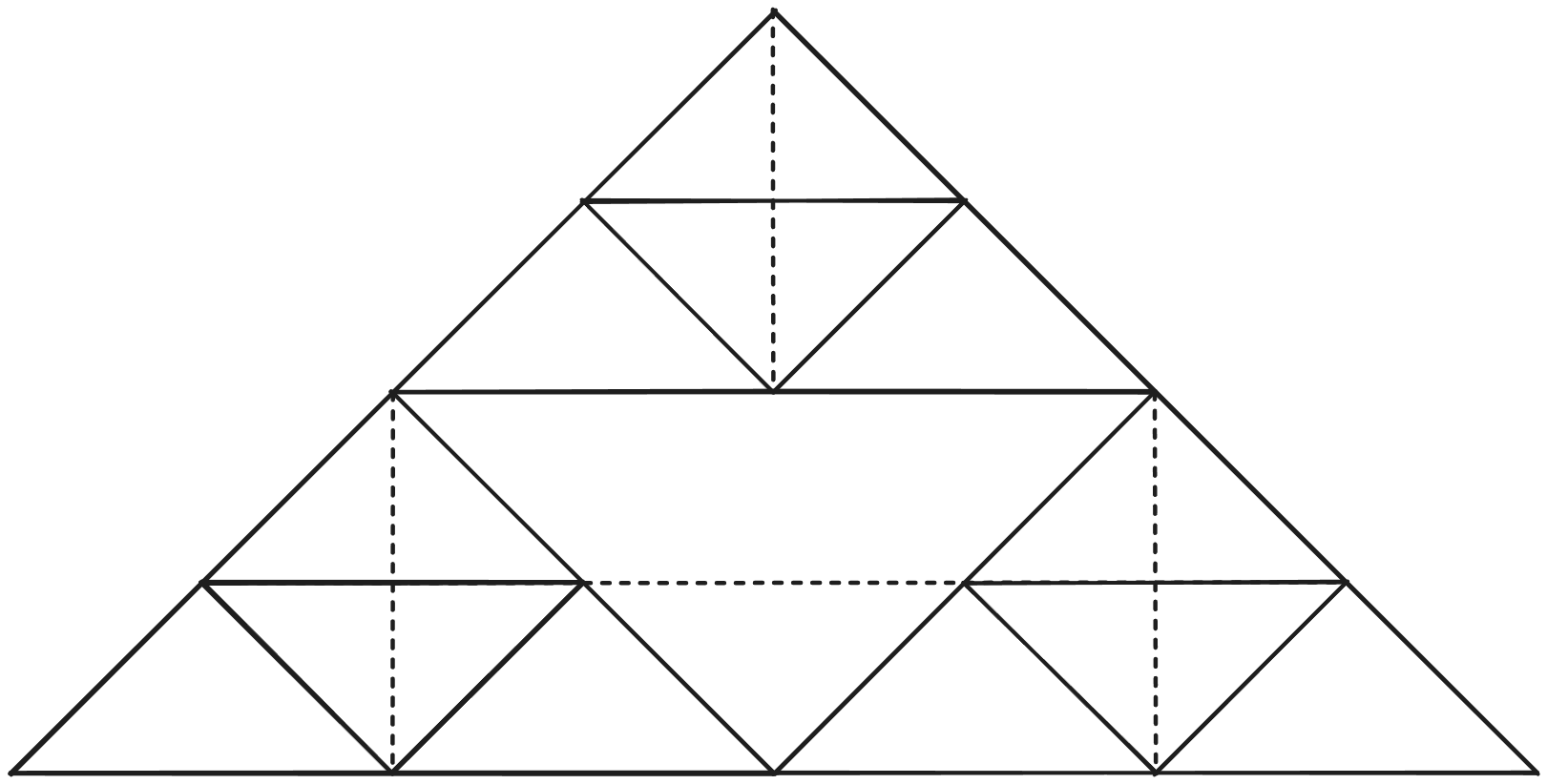
Esta es la iteración sin proyecciones, y lo primero que haré es marcar los ángulos de cada triángulo. Los triángulos que formamos en cada iteración son congruentes, y eso incluye ángulos. Teniendo ángulos congruentes, sabemos que si los proyectamos coincidirá con los del triángulo superior; todas las líneas están con un ángulo de α un medio (α partido en dos).
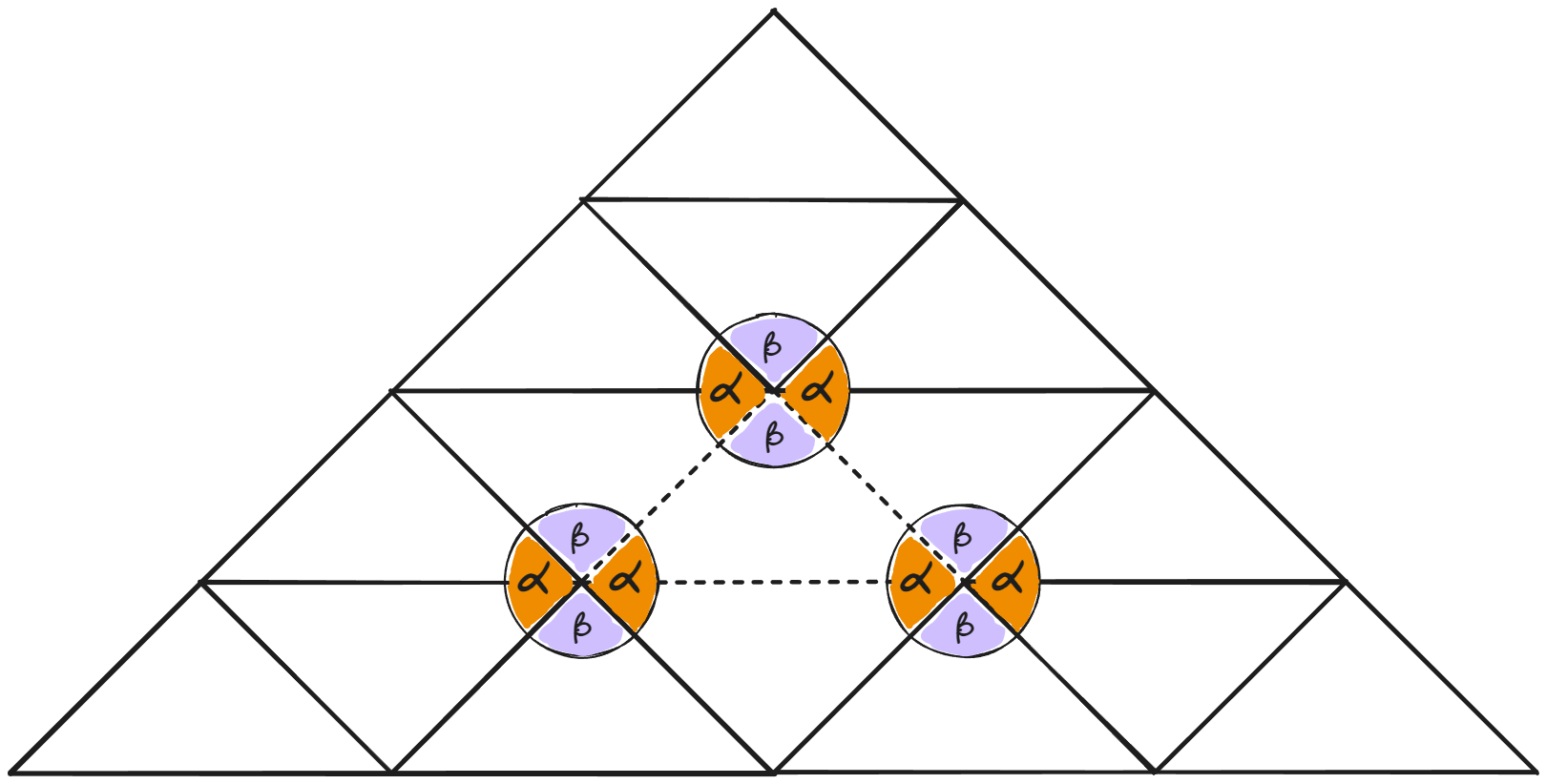
Si te cuesta visualizarlo, las proyecciones coinciden porque tienen la misma "elevación", o, ángulo. Apuntan al mismo lugar.
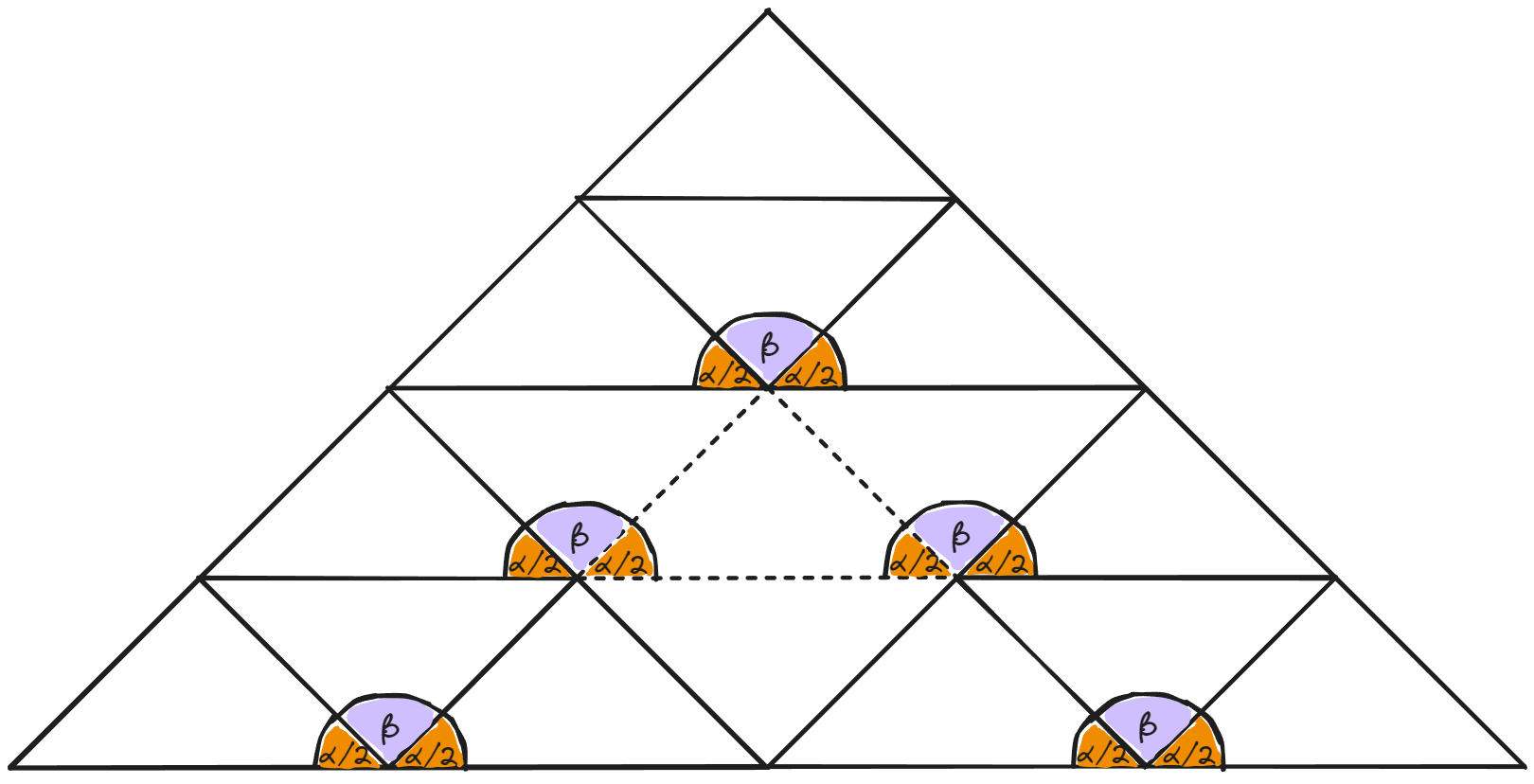
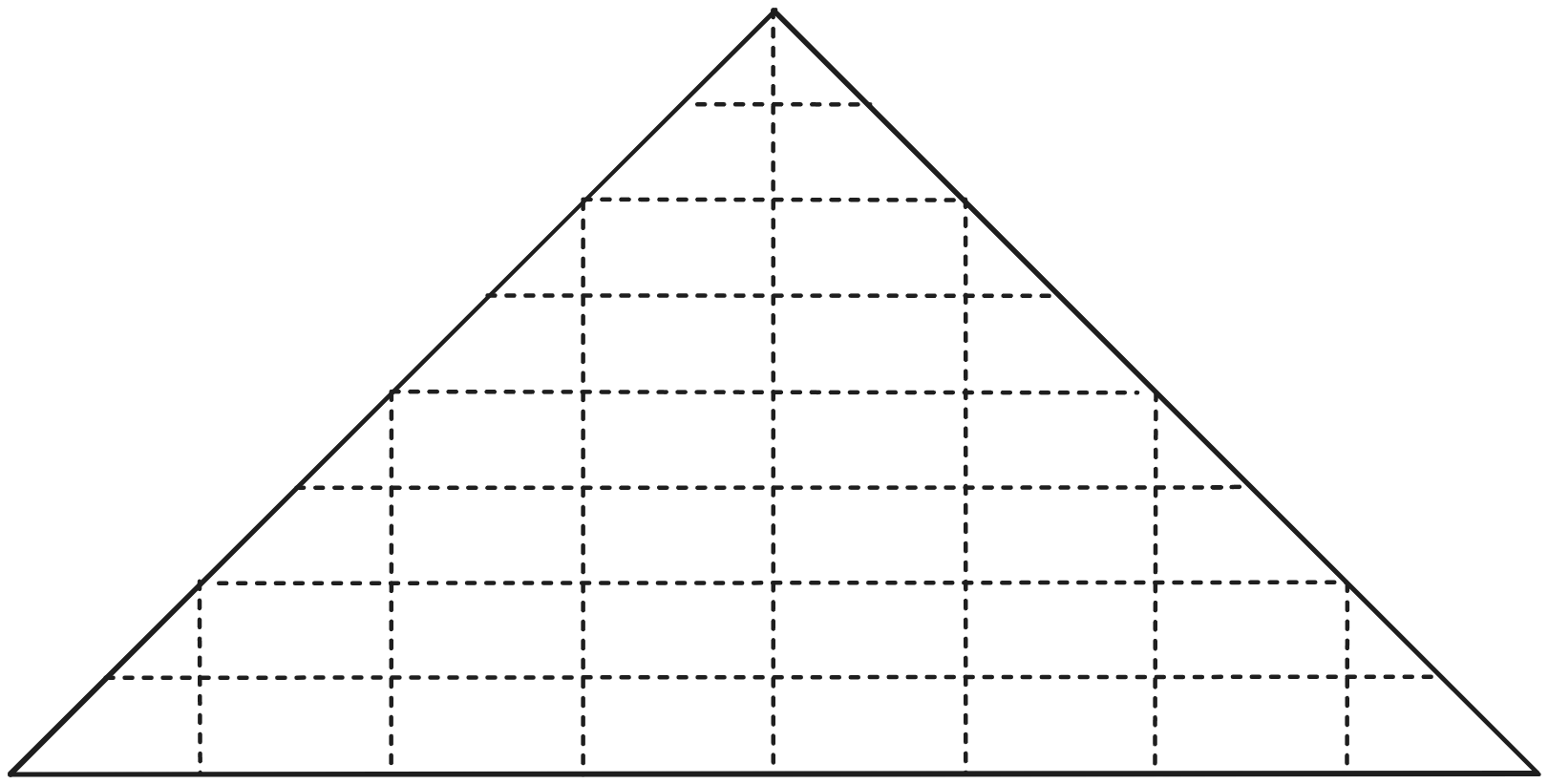
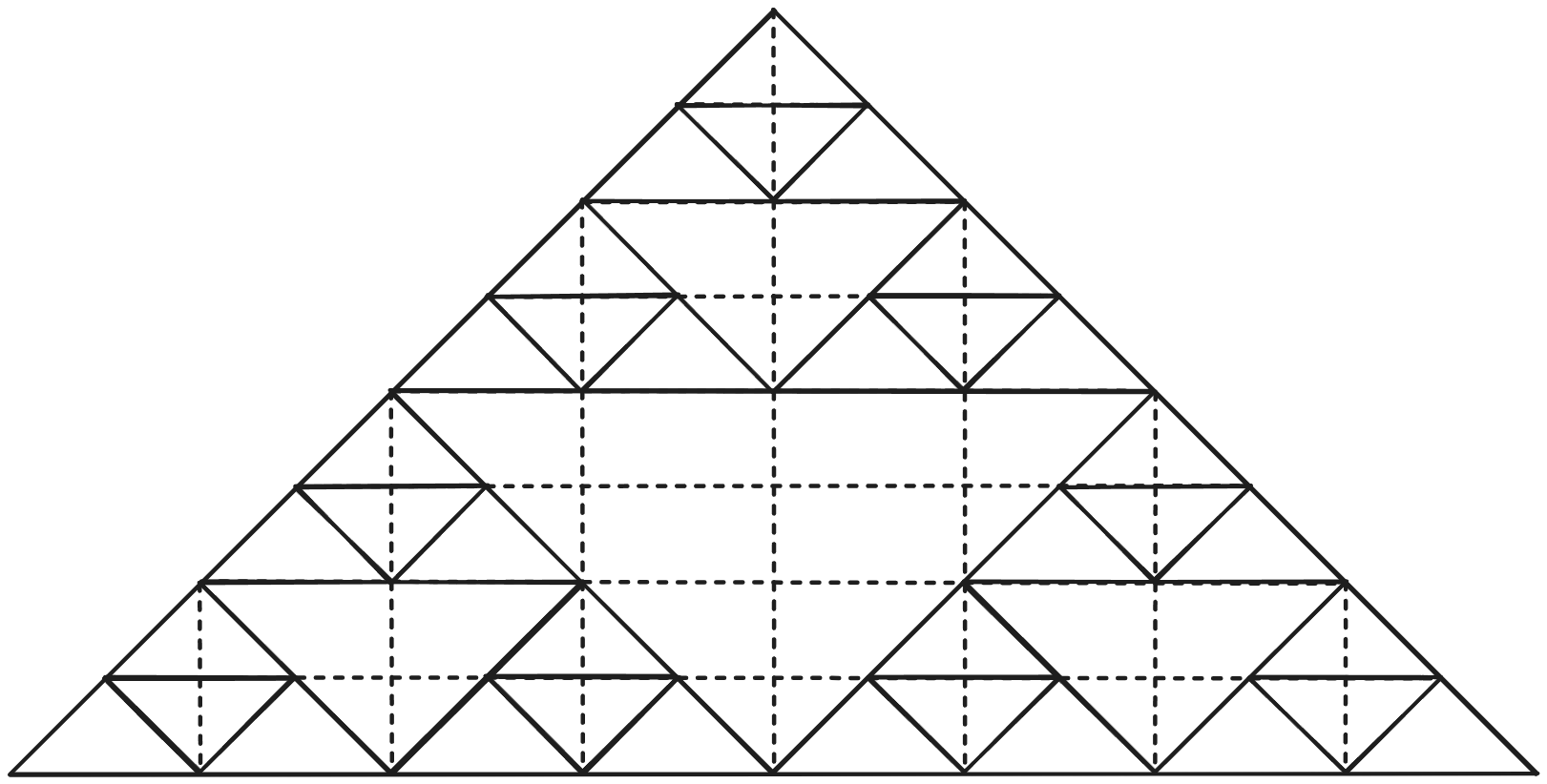
Por último, solo quiero mostrar como se ve un triángulo con solamente las proyecciones y con trazos junto a proyecciones (Sierpinski con tres iteraciones).
