Buenos días, hoy les mostrare tiras pitagóricas, un bonito dibujo que me invente en clases. Son literalmente tiras, pero formadas a partir de cuadrados extendidos de un triángulo rectángulo. Eso suena raro, pero realmente es muy simple y esta completamente basado en el teorema de Pitágoras.

El teorema de Pitágoras nos dice que si sumamos los cuadrados de los lados más cortos de un triángulo rectángulo (catetos), tendremos el cuadrado del lado mas largo (hipotenusa). Esto puede ser tomado literalmente, cuando elevamos algo a dos es hacer un cuadrado.

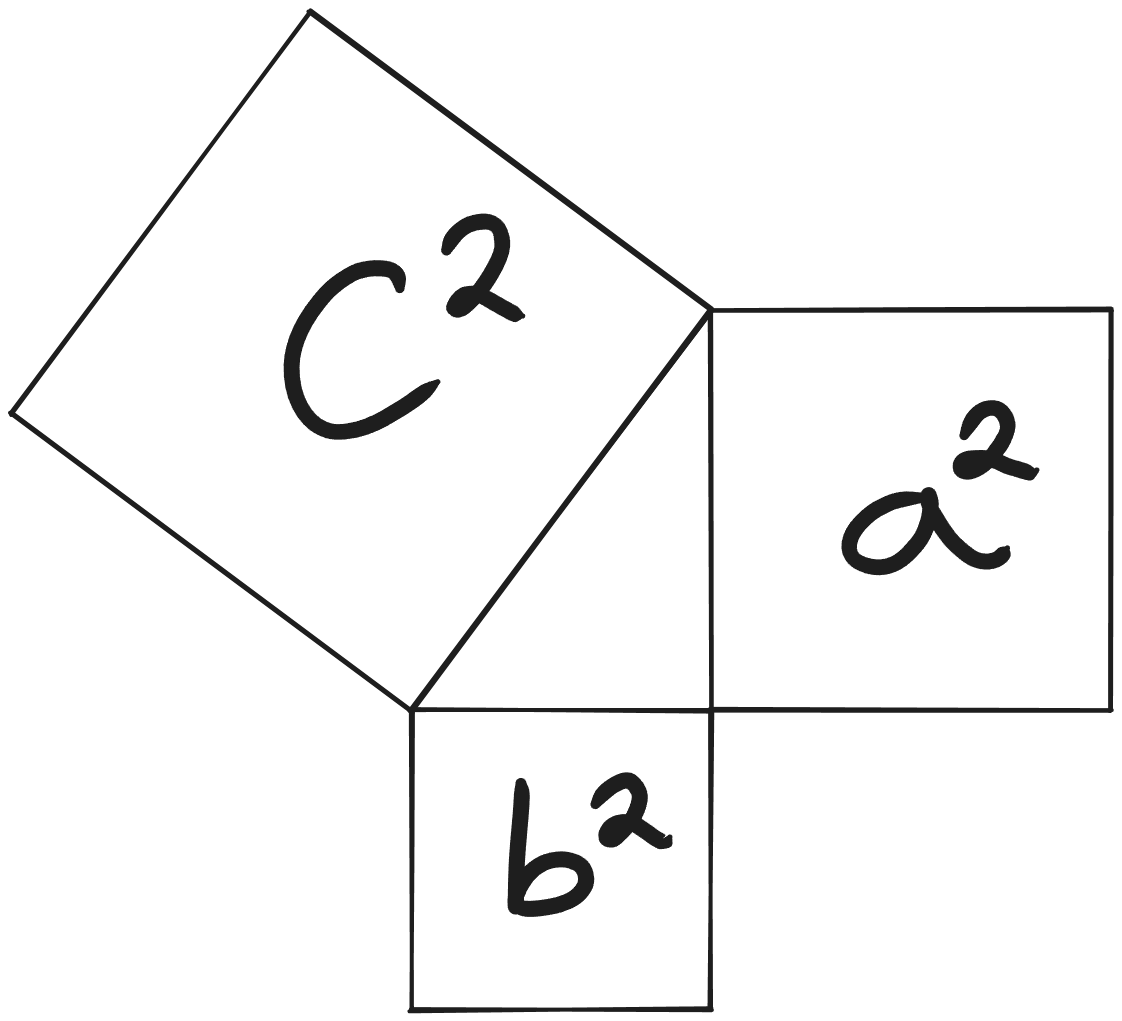
Ahora, si tenemos unos valores numéricos y reordenamos los cuadrados en uno solo, vemos lo siguiente. Como nota, los grupos que cumplen con la condicion definida en el parrafo anterior se denominan ternas o trios pitagóricos/as.

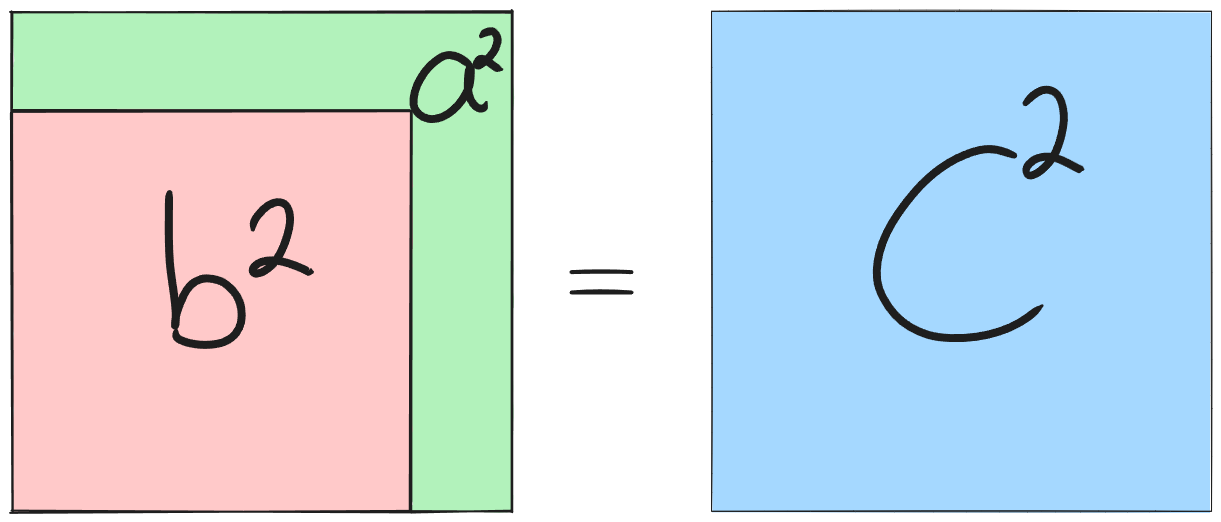
Ahora conociendo el teorema de Pitágoras, podemos empezar. Primero hay que entender que las tiras seran producidas por un proceso iterativo, se repetira multiples veces, las que queramos. Dire que se completo una iteración cuando completemos un triángulo rectángulo extendido, su reflexión y unamos todos los vertices exteriores de cada figura.

Empezaremos dibujando un triángulo rectángulo común, lo hare de lados tres, cuatro y, siguiendo el teorema de Pitágoras, cinco (probablemente mi trio pitagórico favorito).

Lo siguiente es la reflexión de la figura inicial. Nos apoyamos del lado a y b que ya hicimos, sigue teniendo las mismas medidas gracias a ello.

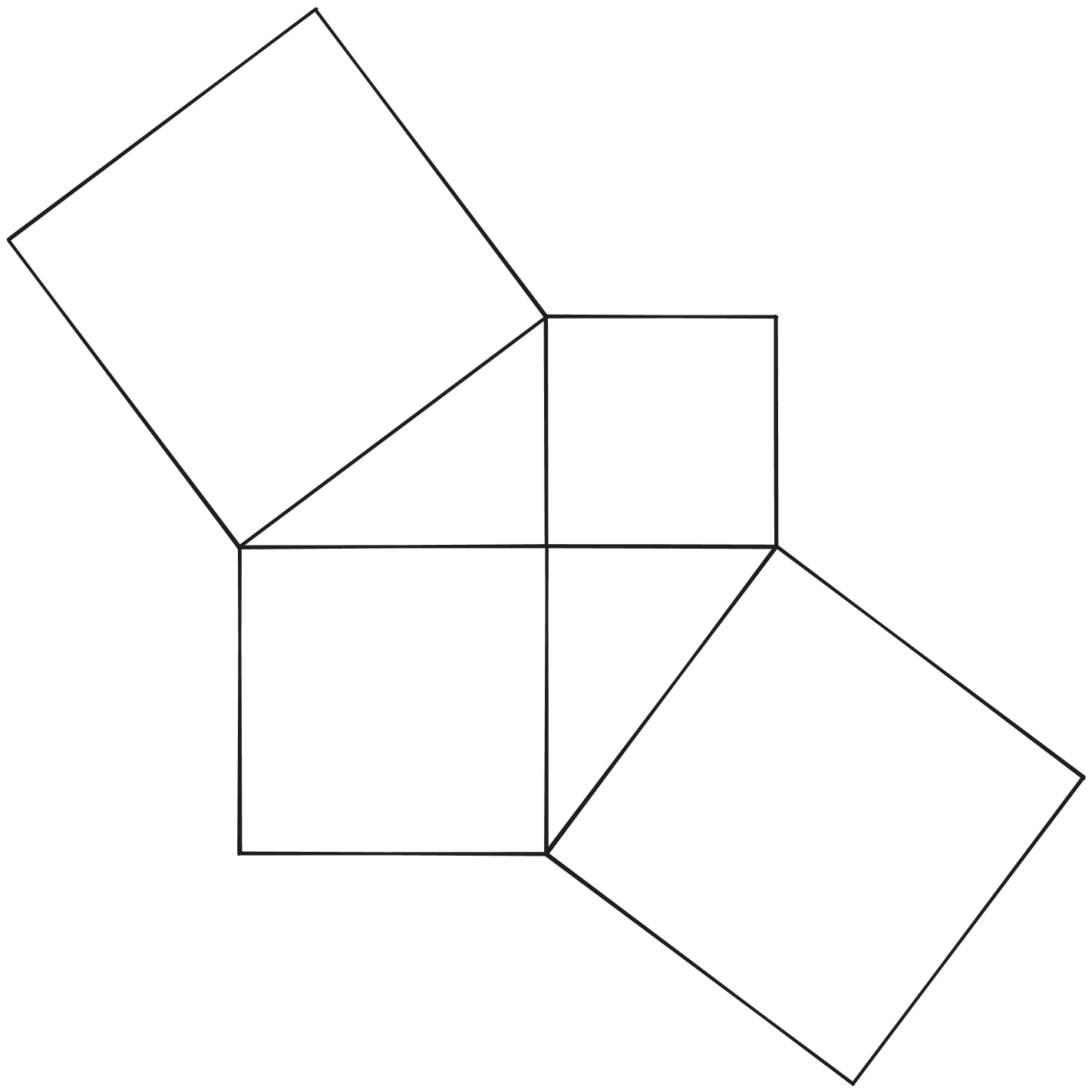
Acá estoy uniendo los vertices exteriores.

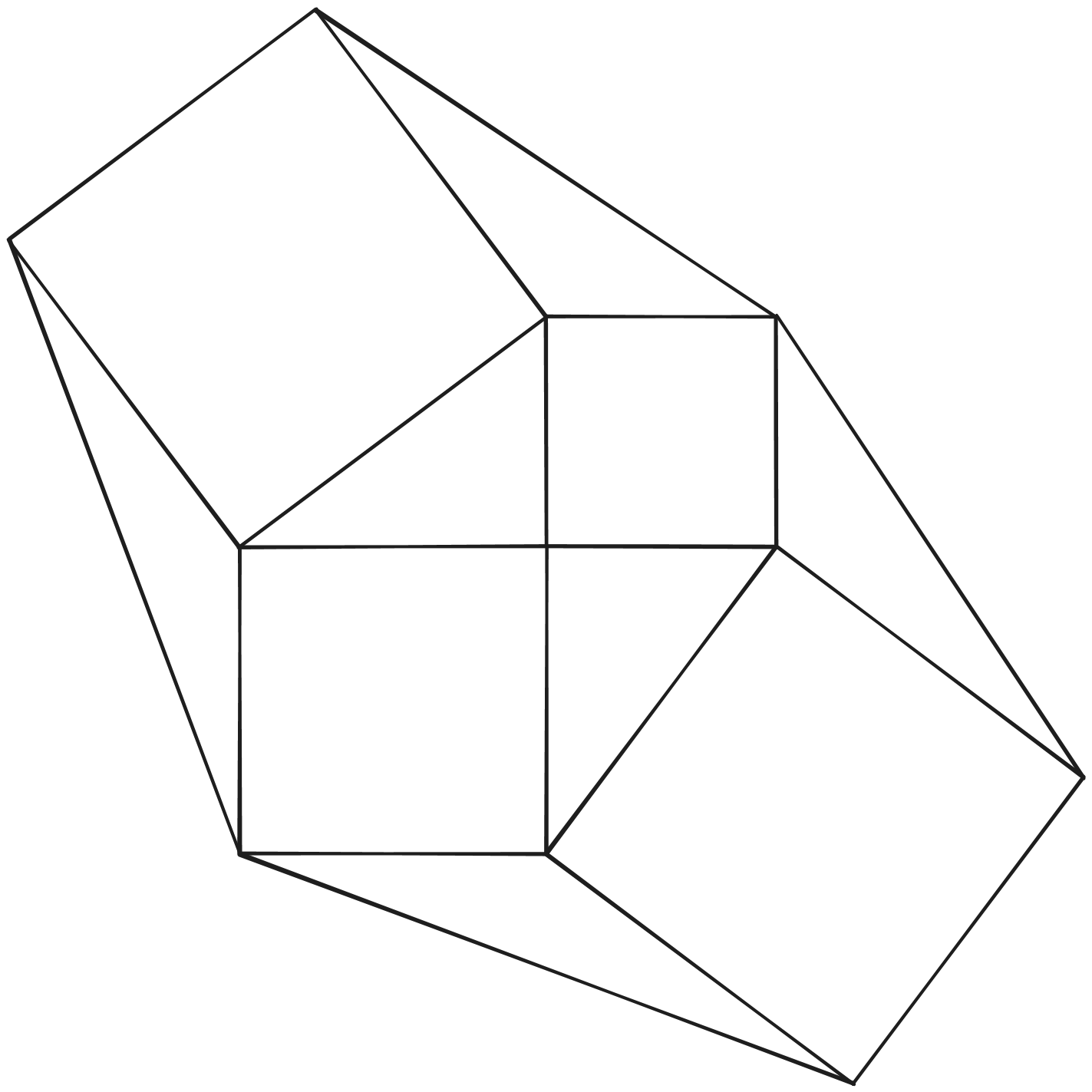
Conociendo el proceso, ahora lo repetire una vez más, solo para que se aprecie bien y continuar a la área total.

Calculo de áreas

(Me he estado rompiendo la cabeza unos días hasta que vi que todo esto se podia simplificar)

Después de definir el proceso para generar una tira, intentaré derivar una fórmula general para poder calcular el área de esta. Lo primero que haré es rellenar los cuadrados y calcular el área total de solo ellos. Para esto usaré la tira de dos iteraciones que hice anteriormente.

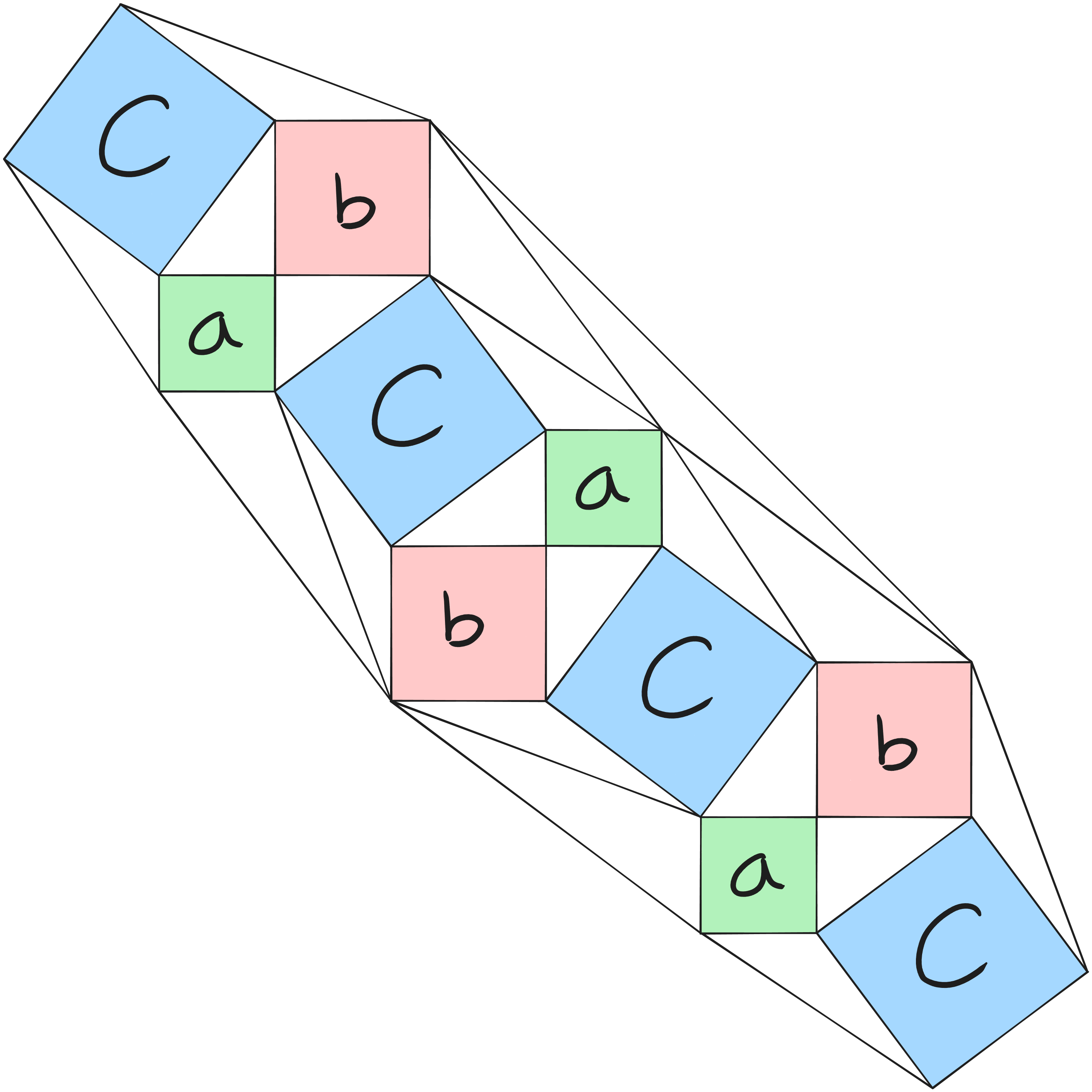
Para calcular el área podemos utilizar el hecho de que por cada iteración obtenemos dos c² nuevos y el a² y b². De lo anterior se sigue que hay 2c²i + a²i + b²i. Ahora, siempre va a haber un segmento central de dos cuadrados a² y b², por lo tanto, tenemos que 2c²i + a²i + b²i + a² + b² que simplificando y factorizando es igual a 2c²i + (a² + b²)(i + 1).

Ahora, con el área de los cuadrados calculada, seguimos con los rectángulos para tener el área total. Como primera nota, los triángulos centrales, los que se forman con los cuadrados a, b y c, son generados dos veces por iteración, y sabiendo que son triángulos rectángulos, su área será CA • 1/2, dando 2c²i + (a² + b²)(i + 1) + CA(i + 1), eso ya habiendo cancelado el un medio con el dos de la iteración, y habiendo sumado los dos triángulos centrales y factorizando.

Un problema son los triángulos escalenos que se encuentran en las afueras, cuyas áreas son pqh/2, pero eso solo usando notación. Los cálculos de tales áreas no los pude encontrar, aunque seguro hay algún teorema o principio de geometría que pueda ayudar, será todo por hoy.